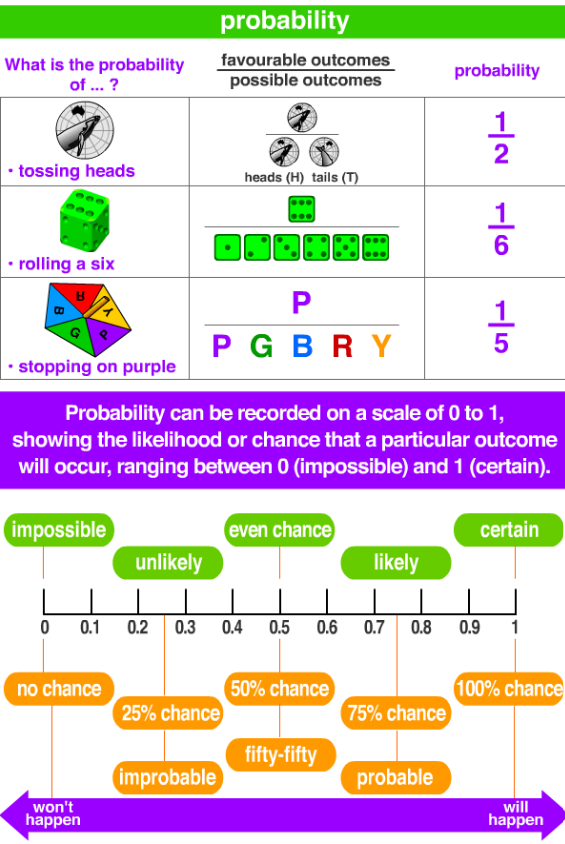
Probability
Probability is a branch of mathematics that deals with the likelihood of different outcomes. It's a measure of how likely an event is to occur and is quantified as a number between 0 and 1.
Definitions related to probability:
Experiment: An action or process that leads to one or several possible outcomes. For example, rolling a die or flipping a coin.
Sample Space (S): The set of all possible outcomes of an experiment. For example, the sample space for rolling a six-sided die is {1, 2, 3, 4, 5, 6}.
Event (E): A subset of the sample space. An event represents one or more outcomes. For example, getting an even number when rolling a die is an event: {2, 4, 6}.
Probability of an Event (P(E)): The likelihood of an event occurring, defined as the ratio of the number of favorable outcomes to the total number of possible outcomes.
Complementary Event: The complement of an event E is the event that E does not occur, denoted as E'. The probability of the complement is:
Union of Events: The probability that at least one of two events occurs. For two events A and B, the union is denoted as A∪B
Intersection of Events: The probability that two events both occur. For two events A and B, the intersection is denoted as A∩B
Conditional Probability: The probability of an event given that another event has occurred, denoted as P(A∣B)
Bayes' Theorem: A formula that relates the conditional and marginal probabilities of random events. It is given by:
Random Variable: A variable that takes on numerical values determined by the outcome of a random phenomenon.
Probability Distribution: A function that describes the likelihood of each possible value of a random variable.
Types of Probability Distributions
- Discrete Probability Distribution: Applies to scenarios where the set of possible outcomes is discrete (e.g., rolling a die).
- Continuous Probability Distribution: Applies to scenarios where the set of possible outcomes is continuous (e.g., measuring the height of people).
Examples
Understanding probability is fundamental in various fields such as statistics, finance, science, and engineering, where it is used to model uncertainty and make informed decisions based on data.