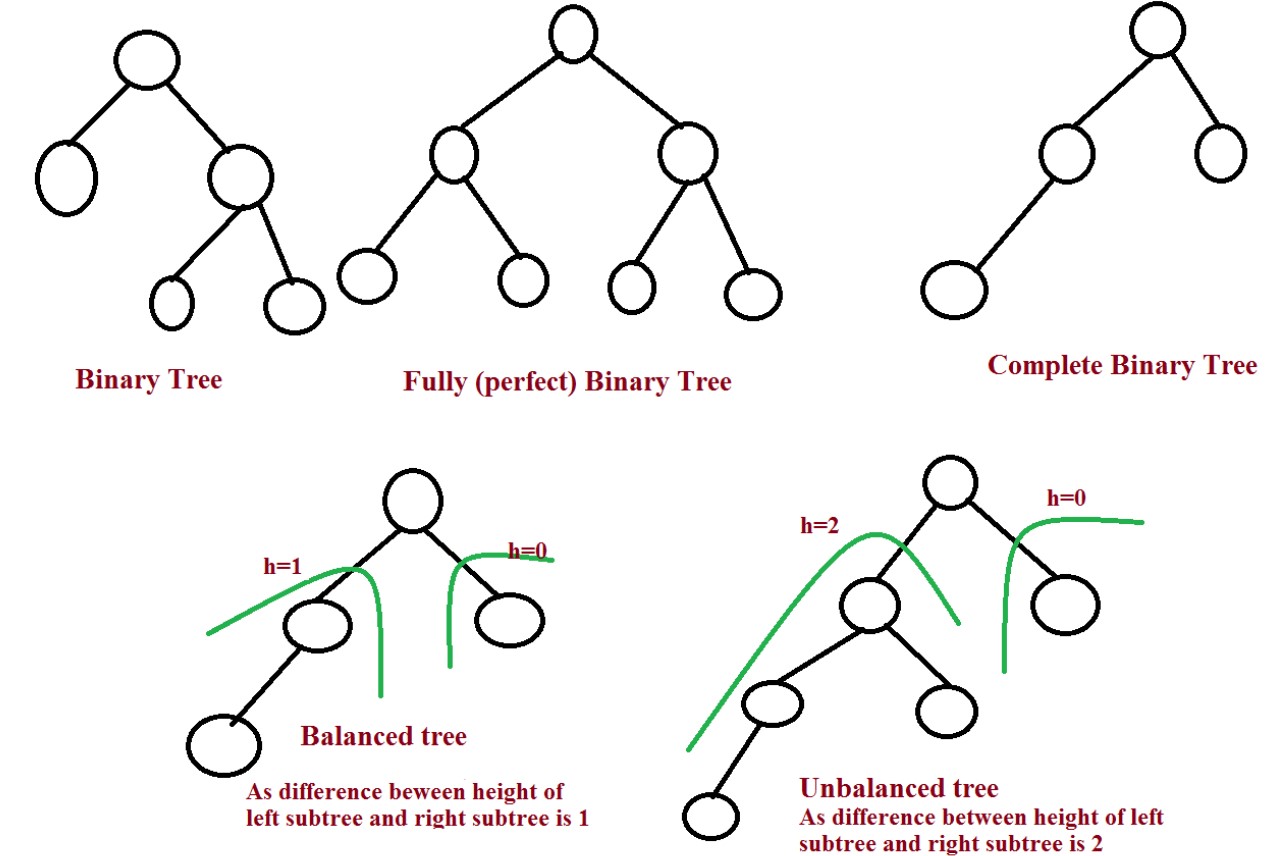
Binary tree
A binary tree is a fundamental data structure in computer science used to organize and store data in a hierarchical manner.
It consists of nodes connected by edges, where each node has at most two child nodes, typically referred to as the left child and the right child.
Some key terms associated with binary trees:
-
Node: Each element in a binary tree is called a node. A node contains some data (or payload) and can have references to its left and right children.
-
Root: The topmost node in a binary tree is called the root node. It is the starting point when traversing the tree.
-
Parent: A node that has child nodes is called a parent node. For example, the root node is a parent to its immediate child nodes.
-
Child: The nodes directly connected to a parent node are called its child nodes. A parent can have zero, one, or two children in a binary tree.
-
Leaf: Nodes that have no children are called leaf nodes or terminal nodes.
-
Subtree: A subtree is a smaller binary tree formed by selecting a node and all its descendants.
-
Depth: The depth of a node is the number of edges on the path from the root node to that node.
-
Height: The height of a binary tree is the maximum depth of any node in the tree. The height of an empty tree is typically defined as -1.
Binary trees are commonly used to implement various data structures and algorithms, such as binary search trees (BSTs) and heaps.
-
Binary Search Tree (BST): A binary search tree is a binary tree that satisfies the following property: for each node, all nodes in its left subtree have values less than the node's value, and all nodes in its right subtree have values greater than the node's value. This property allows for efficient searching, insertion, and deletion operations.
-
Heap: A heap is a binary tree that satisfies the heap property. In a max-heap, the value of each node is greater than or equal to the values of its children, making the root node the maximum element. In a min-heap, the value of each node is less than or equal to the values of its children, making the root node the minimum element. Heaps are often used in priority queues and sorting algorithms like heapsort.
Binary trees come in various forms and variations, each with its own use cases and properties.
Some variations include balanced binary trees (like AVL trees and Red-Black trees) that ensure the tree remains balanced for efficient operations, and full binary trees where every node has either 0 or 2 children.
Traversal algorithms like inorder, preorder, and postorder are used to visit nodes in a binary tree in a specific order, enabling various operations and analyses on the tree's structure and data.
Let's explore a simple example of a binary tree with some explanations.
Consider the following binary tree:
5
/ \
3 8
/ \ \
1 4 10
In this example, the numbers represent the values stored in each node.
- The root node has the value 5.
- The left child of the root has the value 3, and its left and right children have the values 1 and 4, respectively.
- The right child of the root has the value 8, and its right child has the value 10.
Let's look at some key terms and concepts in relation to this binary tree:
-
Root: The root node is 5.
-
Parent and Children: The parent-child relationships are as follows:
- Node 5 (root) is the parent of nodes 3 (left child) and 8 (right child).
- Node 3 (left child) is the parent of nodes 1 (left child) and 4 (right child).
- Node 8 (right child) is the parent of node 10 (right child).
-
Leaves: The leaf nodes are nodes 1, 4, and 10 because they have no children.
-
Depth and Height:
- The depth of node 5 is 0, as it's the root.
- The depth of nodes 3 and 8 is 1.
- The depth of nodes 1, 4, and 10 is 2.
- The height of the tree is 2, as the longest path from the root to a leaf is 2 edges.
-
Subtrees:
- The subtree rooted at node 3 consists of nodes 1 and 4.
- The subtree rooted at node 8 consists of only node 10.
-
Binary Search Property: If this tree were a binary search tree (BST), each node's value on the left would be less than the parent's value, and each node's value on the right would be greater. In this example, the tree is not a BST since node 8 is to the right of node 5, violating the property.
-
Traversal:
- Inorder traversal: 1, 3, 4, 5, 8, 10
- Preorder traversal: 5, 3, 1, 4, 8, 10
- Postorder traversal: 1, 4, 3, 10, 8, 5
This example provides a visual representation of a binary tree and helps illustrate the concepts related to binary trees and their structures.
Keep in mind that binary trees can take many forms, and their properties can vary based on their specific arrangements of nodes and values.