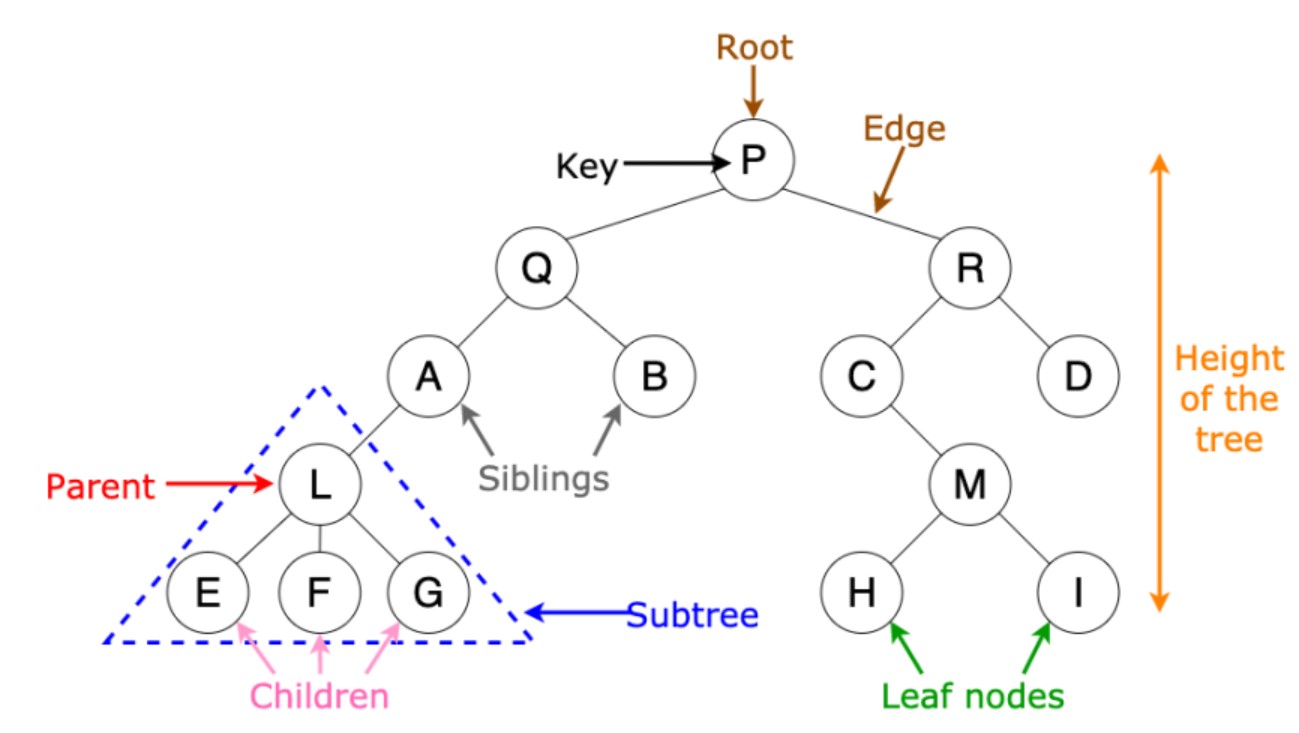
Binary Search Tree (BST)
A Binary Search Tree (BST) is a type of binary tree that has an important property: for each node, all nodes in its left subtree have values less than the node's value, and all nodes in its right subtree have values greater than the node's value. This property allows for efficient searching, insertion, and deletion operations.
The structure of a BST helps in maintaining the order of the elements, making it suitable for tasks such as searching for a specific element, finding the minimum or maximum element, and performing range queries.
Example of a Binary Search Tree:
8
/ \
3 10
/ \ \
1 6 14
/ \ /
4 7 13
In this example, each node follows the BST property:
- Node 8 has nodes 3 and 10 as its children, with 3 in the left subtree and 10 in the right subtree.
- Node 3 has nodes 1 and 6 as its children, with 1 in the left subtree and 6 in the right subtree.
- Node 6 has nodes 4 and 7 as its children, with 4 in the left subtree and 7 in the right subtree.
- Node 10 has node 14 as its right child.
- Node 14 has node 13 as its left child.
Key operations and characteristics of Binary Search Trees:
-
Searching: Searching in a BST is efficient. You start at the root and compare the target value with the current node's value. If they match, you've found the element. If the target is less, you move to the left child; if it's greater, you move to the right child. Repeat until you find the element or reach a null node.
-
Insertion: To insert an element into a BST, you traverse the tree as you would during a search to find the appropriate location for the new node based on its value. Once you reach an empty spot (a null link), you insert the new node.
-
Deletion: Deleting a node can be a bit more complex. There are three cases to consider:
- Node has no children: Simply remove the node.
- Node has one child: Remove the node and replace it with its child.
- Node has two children: Replace the node with its in-order successor (smallest node in the right subtree) or in-order predecessor (largest node in the left subtree), and then delete that successor or predecessor node.
-
In-order Traversal: In-order traversal of a BST visits the nodes in sorted order. It involves visiting the left subtree, then the root node, and finally the right subtree.
-
Minimum and Maximum: The minimum element in a BST is the leftmost leaf node, and the maximum element is the rightmost leaf node.
-
Balanced BST: For optimal performance, you often want to ensure that the tree remains balanced (the heights of the left and right subtrees are similar). Various balanced BSTs like AVL trees and Red-Black trees are used to maintain this balance.
Binary Search Trees are a fundamental data structure in computer science due to their efficient operations, and they have applications in databases, searching algorithms, and more.