Navie Bayes Algorithm
Naive Bayes is a popular machine learning algorithm for classification and probabilistic modeling.
It is based on Bayes' theorem, which is a probability theory used to make predictions based on prior knowledge of conditions that might be related to an event.
The "naive" in Naive Bayes comes from the assumption of independence between features, which simplifies the modeling process. Despite its simplicity, Naive Bayes is surprisingly effective in many real-world applications, such as text classification, spam detection, and sentiment analysis.
Key concepts and workings of the Naive Bayes algorithm:
-
Bayes' Theorem:
- Bayes' theorem is used to calculate conditional probabilities. It relates the probability of an event A occurring given that an event B has occurred to the probability of event B occurring given that event A has occurred.
-
Naive Assumption:
- The "naive" assumption in Naive Bayes is that all features used in the classification are independent of each other. This means that the presence or absence of a particular feature does not affect the presence or absence of any other feature.
-
Bayesian Probability:
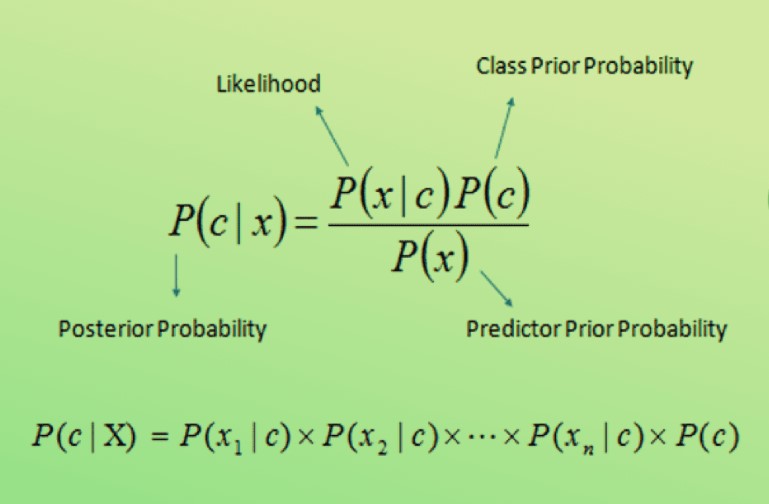
- In the context of Naive Bayes, Bayes' theorem is used to calculate the posterior probability of a class given a set of features. This is done using the following formula:
- P(C_k|X) is the posterior probability of class C_k given the features X.
- P(X|C_k) is the likelihood of observing the features X given class C_k.
- P(C_k) is the prior probability of class C_k.
- P(X) is the evidence probability (a normalization constant).
-
Classification:
- To classify a new data point, Naive Bayes calculates the posterior probability for each class and selects the class with the highest probability as the predicted class.
-
Types of Naive Bayes:
- There are several variants of Naive Bayes, depending on the nature of the data and the distribution of features. Common variants include:
- Gaussian Naive Bayes: Assumes that features follow a Gaussian (normal) distribution.
- Multinomial Naive Bayes: Suitable for discrete data, often used in text classification with word counts.
- Bernoulli Naive Bayes: Applicable to binary data, where features are either present or absent.
- There are several variants of Naive Bayes, depending on the nature of the data and the distribution of features. Common variants include:
-
Laplace Smoothing (Additive Smoothing):
- To handle the problem of zero probabilities when a feature is not present in the training data for a particular class, Laplace smoothing is often applied. It adds a small constant to all counts to avoid zero probabilities.
-
Applications:
- Naive Bayes is commonly used in text classification tasks like spam detection, sentiment analysis, and document categorization. It's also used in recommendation systems and fraud detection.
Despite its "naive" assumptions about feature independence, Naive Bayes can perform surprisingly well on a wide range of tasks, especially when the dataset is relatively large and the features are not highly dependent on each other.
It is computationally efficient and requires minimal tuning compared to more complex models. However, its performance may suffer when the independence assumption is significantly violated.