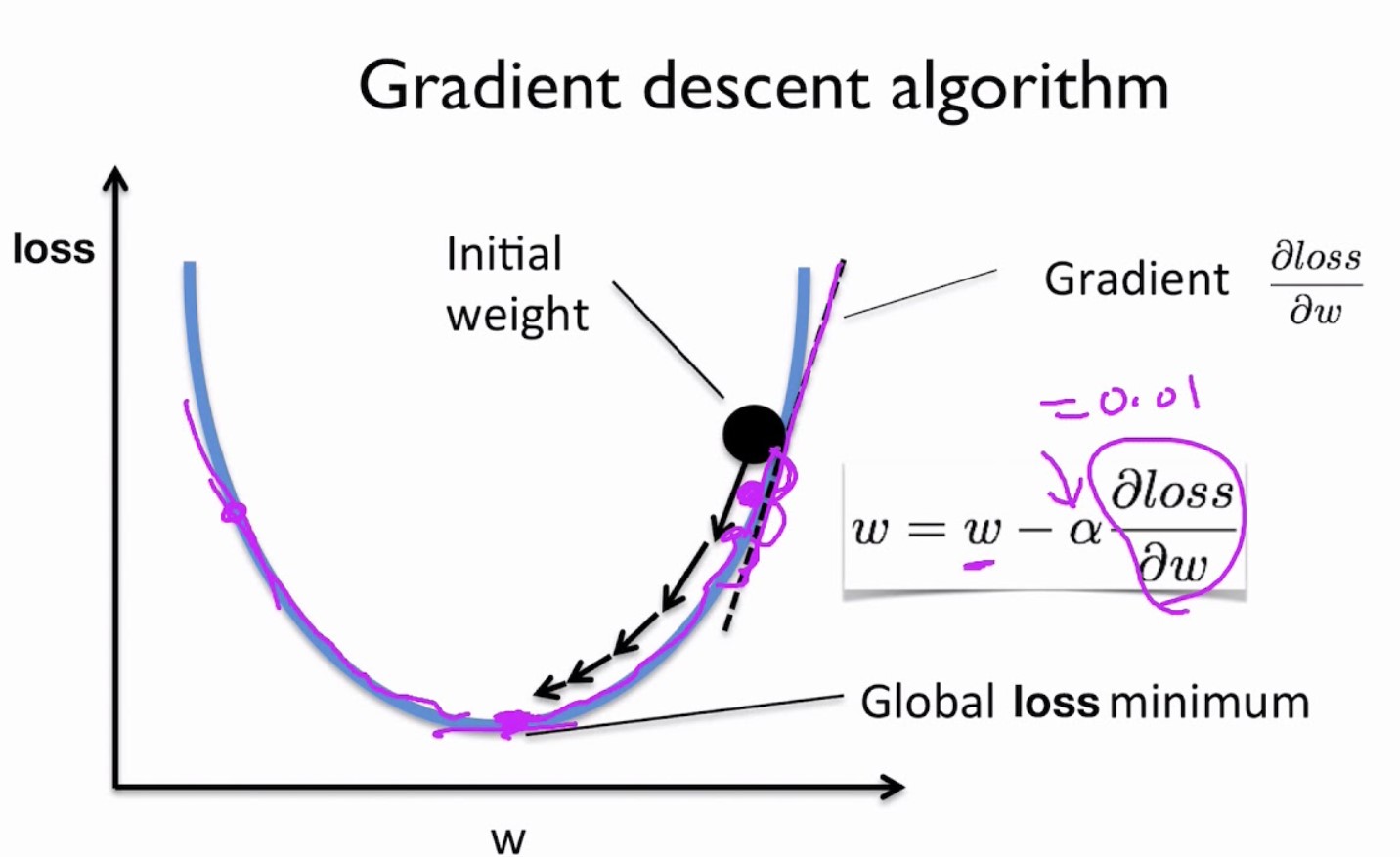
Gradient Descent
Gradient Descent is a fundamental optimization algorithm used in deep learning and machine learning to minimize a loss function and update the model's parameters during training. It is a core component of the training process, allowing neural networks to learn from data. Here's an overview of Gradient Descent in the context of deep learning:
-
Objective Function:
- In deep learning, the primary goal is to minimize an objective function, often referred to as the loss function or cost function. This function quantifies the difference between the predicted outputs of a model and the actual target values.
-
Gradient:
- The gradient of the objective function with respect to the model's parameters is a vector that points in the direction of the steepest increase in the function.
- In other words, the gradient indicates how the loss will change as each parameter is adjusted.
-
Learning Rate:
- The learning rate (often denoted as "α") is a hyperparameter that controls the step size or the size of the updates applied to the model's parameters in each iteration of the optimization process.
- It is a critical hyperparameter because it determines how quickly or slowly the model converges to a solution.
-
Gradient Descent Process:
- The Gradient Descent process starts with an initial set of model parameters.
- In each iteration (also called an epoch), the following steps are performed:
- Compute the gradient of the loss function with respect to the parameters.
- Update the parameters in the opposite direction of the gradient to minimize the loss:
θ_new = θ_old - α * gradient - Repeat these steps until a stopping criterion is met (e.g., a maximum number of iterations, convergence to a minimum loss).
-
Batch Gradient Descent:
- In batch gradient descent, the entire training dataset is used to compute the gradient in each iteration.
- It provides accurate estimates of the gradient but can be computationally expensive for large datasets.
-
Stochastic Gradient Descent (SGD):
- In stochastic gradient descent, only a single randomly selected training sample is used to compute the gradient in each iteration.
- It can be noisy but often converges faster and is computationally more efficient.
-
Mini-Batch Gradient Descent:
- Mini-batch gradient descent strikes a balance between batch gradient descent and stochastic gradient descent.
- It uses a small random subset (mini-batch) of the training data to compute the gradient in each iteration.
- Mini-batch sizes are typically chosen based on hardware constraints and computational efficiency.
-
Convergence:
- Gradient Descent aims to find the parameters that minimize the loss function.
- Convergence is achieved when the loss stops decreasing significantly, or when a predefined convergence criterion is met.
-
Local Minima:
- Gradient Descent can sometimes get stuck in local minima, which are suboptimal solutions.
- Various techniques, such as momentum, learning rate scheduling, and different optimization algorithms (e.g., Adam, RMSprop), are used to mitigate this issue.
Gradient Descent is the foundation of many optimization algorithms used in deep learning. The choice of the optimization algorithm and its hyperparameters can significantly impact the training process and the quality of the learned model. Researchers and practitioners often experiment with different variants of Gradient Descent and optimization strategies to improve model training and convergence.