Probability
Probability is a fundamental concept in statistics that quantifies the likelihood or chance of an event occurring.
It provides a mathematical framework to analyze and understand uncertainty and randomness.
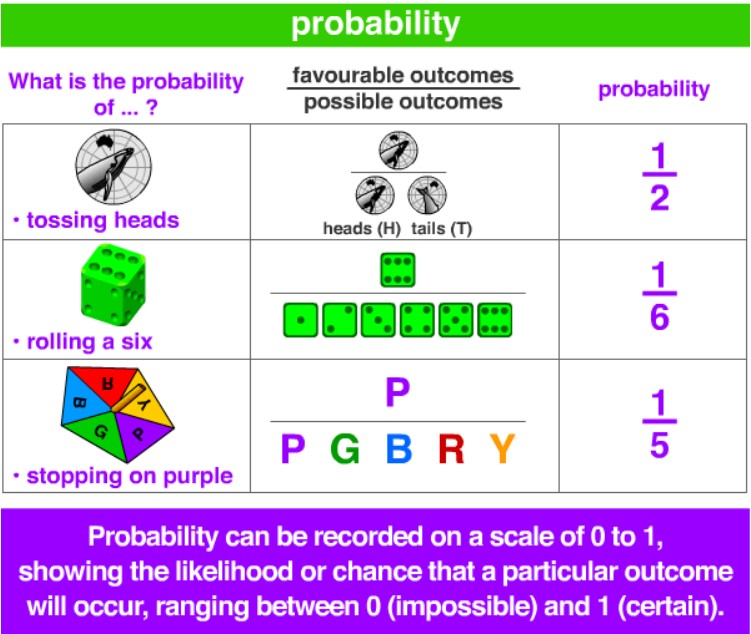
Probability is expressed as a value between 0 and 1, where 0 represents an impossible event, and 1 represents a certain event.
Here are some key concepts related to probability in statistics:
Sample Space: The sample space refers to the set of all possible outcomes of a random experiment.
For example, when flipping a fair coin, the sample space consists of two outcomes: heads (H) and tails (T). Event: An event is a subset of the sample space. It represents a specific outcome or a combination of outcomes.
For instance, in the coin-flipping example, the event of getting heads is a specific outcome within the sample space. Probability of an Event: The probability of an event is a measure of the likelihood of that event occurring.
It is denoted by P(Event) and ranges between 0 and 1. The probability of an event A is calculated by dividing the number of favorable outcomes by the total number of possible outcomes. It can also be determined using relative frequencies from observed data.
Probability Distribution
A probability distribution describes the probabilities associated with different outcomes of a random variable. It provides a systematic way to assign probabilities to events or outcomes. Examples of probability distributions include the binomial distribution, normal distribution, and Poisson distribution.
Rules of Probability
Several rules govern the manipulation and calculation of probabilities, including the addition rule, multiplication rule, and complement rule. These rules help determine the probability of compound events, independent and dependent events, and the probability of the complement of an event.
Conditional Probability
Conditional probability measures the probability of an event occurring given that another event has already occurred. It is denoted as P(A|B), where A and B are two events. Conditional probability is used to analyze dependent events and to update probabilities based on new information.
Bayes' Theorem
Bayes' theorem is a fundamental result in probability theory that allows for the calculation of conditional probabilities. It provides a way to update prior probabilities with new evidence or information.
Probability theory forms the basis of statistical inference, hypothesis testing, and decision-making.
By understanding and applying probability concepts, statisticians can quantify uncertainty, make predictions, analyze data, and draw meaningful conclusions from observed outcomes.