Matrix

---

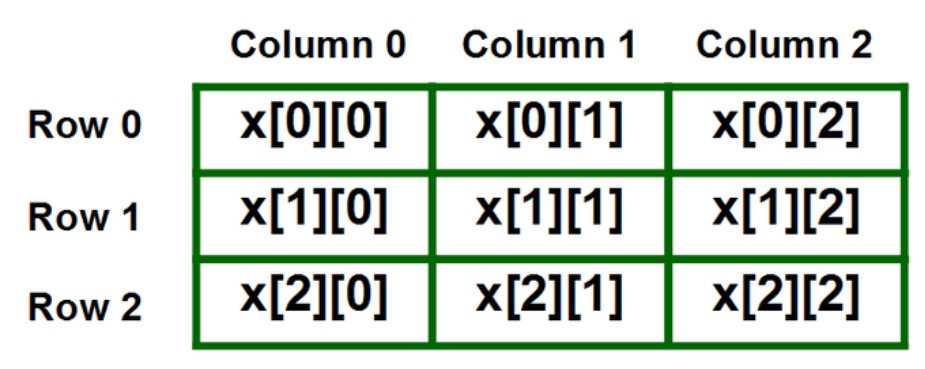
A matrix is a two-dimensional data structure consisting of rows and columns, forming a grid-like arrangement of elements. It's often used to represent tables of data, images, graphs, and various mathematical and computational concepts.

In computer science, matrices are widely used to solve linear algebraic equations, perform transformations, represent graphs and networks, and handle data in applications like image processing, machine learning, and simulations.

Example of a simple 3x3 matrix:

| 1  2  3 |
| 4  5  6 |
| 7  8  9 |

In this matrix:

• Rows are horizontal sequences of elements: [1, 2, 3], [4, 5, 6], and [7, 8, 9].
• Columns are vertical sequences of elements: [1, 4, 7], [2, 5, 8], and [3, 6, 9].

Matrices can be classified based on their properties:

1. Square Matrix: A matrix where the number of rows is equal to the number of columns (rows = columns). For example, a 3x3 matrix is a square matrix.

2. Rectangular Matrix: A matrix where the number of rows is not equal to the number of columns.

3. Row Matrix: A matrix with only one row.

4. Column Matrix: A matrix with only one column.

5. Identity Matrix: A square matrix with ones on the main diagonal and zeros elsewhere. It behaves like the number "1" in matrix multiplication.

6. Diagonal Matrix: A square matrix where all non-diagonal elements are zero.

7. Upper Triangular Matrix: A square matrix where all elements below the main diagonal are zero.

8. Lower Triangular Matrix: A square matrix where all elements above the main diagonal are zero.

9. Transpose: The transpose of a matrix is obtained by interchanging rows and columns.

Matrix operations include addition, subtraction, multiplication, and scalar multiplication. Matrix multiplication is a fundamental operation used in many applications, but it's important to note that it's not commutative (AB ≠ BA in most cases).

In programming, matrices can be implemented using arrays or nested lists. Libraries like NumPy in Python provide powerful tools for working with matrices and performing various matrix operations efficiently.

Overall, matrices are a foundational concept in computer science and mathematics, with wide-ranging applications in various fields.

Example of a matrix represented as a 3x3 grid of numbers:

| 2  4  6 |
| 1  3  5 |
| 7  9 11 |

In this matrix:

• Rows: There are 3 rows.
• Columns: There are 3 columns.

You can access elements in the matrix using row and column indices. For example, the element in the first row and second column (row index 0, column index 1) is 4.

Matrix operations in this example:

1. Addition:

   | 2  4  6 |   | 1  0 -1 |   | 3  4  5 |
   | 1  3  5 | + | 2  1  0 | = | 3  4  5 |
   | 7  9 11 |   | 0  2  3 |   | 7 11 14 |
   

    

2. Scalar Multiplication (Multiply by 2):

   |  4  8 12 |
|  2  6 10 |
| 14 18 22 |

3. Matrix Multiplication (with another 3x3 matrix):

   | 2  4  6 |   | 1  2  3 |   | 20  28  36 |
   | 1  3  5 | x | 4  5  6 | = | 26  37  48 |
   | 7  9 11 |   | 7  8  9 |   | 92 129 166 |
   

    

4. Transpose:

   |  2  1  7 |
   |  4  3  9 |
   |  6  5 11 |
   
   

These are just a few basic matrix operations. Matrices are used in various mathematical computations, graphics processing, linear algebra, image processing, machine learning, and more.

They provide a powerful way to organize and manipulate structured data.

Enroll Now

• Computer Science
• Data Structures