Statistics Mean Median Mode Standard Deviation Interquartile Range Correlation Co-efficient Variation Standard Error Root Mean Square Error Normal Distribution Hypothesis Testing Probability Probability Bayes Theorem Statistics Quiz

Root mean square error (RMSE)

In statistics, root mean square error (RMSE) is a measure of the accuracy of a predictive model or estimator. It quantifies the average difference between the predicted values and the actual values.

RMSE is commonly used in regression analysis and other prediction tasks. RMSE is calculated by taking the square root of the mean of the squared differences between the predicted and actual values.

The formula for calculating RMSE is as follows:

RMSE = sqrt((1/n) * Σ((yi - ŷi)^2)), where yi represents the actual values, ŷi represents the predicted values, n is the total number of observations, and Σ represents the sum of the squared differences.

Let's illustrate the concept of RMSE with an example:

Example: Suppose we have a dataset of actual and predicted sales values for a product over a period of six months.


The actual sales values are:

100, 120, 130, 110, 150, 140.

The corresponding predicted values from a model or estimator are:

90, 110, 120, 100, 130, 135.

To calculate the RMSE for the predicted sales, we follow these steps:

Calculate the squared differences between the actual and predicted values:

(100 - 90)^2 = 100, (120 - 110)^2 = 100, (130 - 120)^2 = 100, (110 - 100)^2 = 100, (150 - 130)^2 = 400, (140 - 135)^2 = 25.

Find the sum of the squared differences:


100 + 100 + 100 + 100 + 400 + 25 = 825.

Divide the sum by the number of observations (n):

825 / 6 = 137.5.

Take the square root of the result to obtain the RMSE:

sqrt(137.5) ≈ 11.72.

The RMSE for the predicted sales values is approximately 11.72.

Interpretation:

The RMSE represents the average difference between the predicted sales values and the actual sales values. It provides a measure of the model's predictive accuracy.

In this example, the RMSE of 11.72 indicates that, on average, the predicted sales values differ from the actual sales values by approximately 11.72 units. RMSE is a widely used metric for evaluating predictive models and estimators. It allows for the comparison of different models and helps assess their performance in accurately predicting or estimating target variables.

Root mean square error (RMSE)


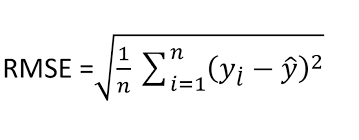
Enroll Now

  • Python Programming
  • Machine Learning