Standard Error
Example: Suppose we want to estimate the average weight of all newborn babies in a hospital. We collect a random sample of 100 newborns and measure their weights.
The sample mean weight is found to be 3.2 kilograms, and the sample standard deviation is 0.4 kilograms.
To estimate the standard error of the mean weight,
we use the formula:
SE = σ / √n, where σ is the population standard deviation and n is the sample size.
In this case, we don't know the population standard deviation, so we'll use the sample standard deviation as an estimate.
Therefore, the standard error can be calculated as follows:
SE = 0.4 / √100 = 0.4 / 10 = 0.04 kilograms.
The standard error of the mean weight is 0.04 kilograms.
Interpretation
The standard error represents the average amount of variation or uncertainty expected in estimating the average weight of all newborns based on the sample. It tells us that the estimated mean weight of 3.2 kilograms may vary by approximately 0.04 kilograms from the true population mean.
The standard error is particularly useful in constructing confidence intervals. For example, if we want to construct a 95% confidence interval for the population mean weight, we would use the sample mean weight of 3.2 kilograms and the standard error of 0.04 kilograms to calculate the margin of error around the estimate.
The standard error provides a measure of the precision of our estimate and helps us understand the variability expected in estimating population parameters from sample data. It is an essential tool in statistical inference and plays a crucial role in interpreting the reliability of statistical estimates.
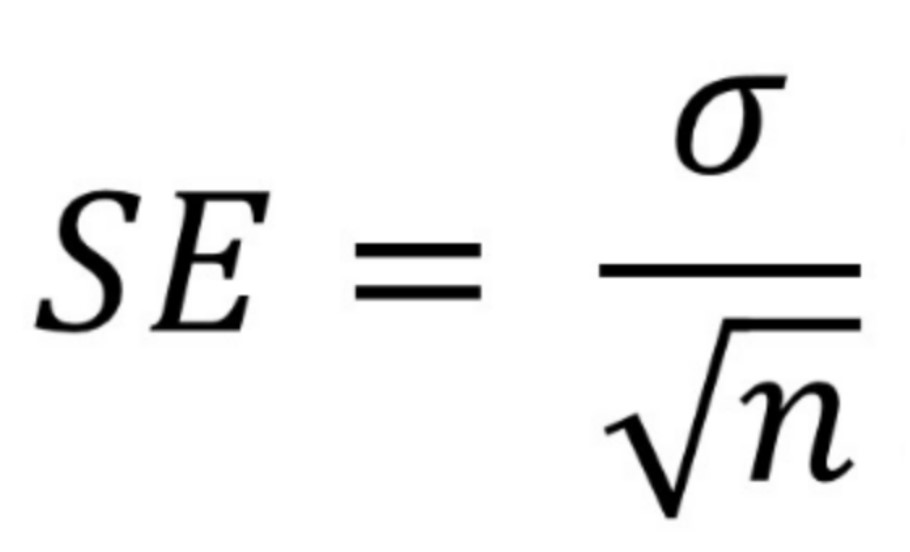
Enroll Now
- Python Programming
- Machine Learning