Precision recall and F1 score
Precision, recall, and the F1 score are important evaluation metrics used in deep learning and machine learning for classification tasks. They provide insights into the performance of a model, especially in situations where imbalanced classes or different costs associated with false positives and false negatives are involved. These metrics are calculated based on the confusion matrix, which consists of four values: true positives (TP), false positives (FP), true negatives (TN), and false negatives (FN).
Detailed explanation of these metrics:
Precision
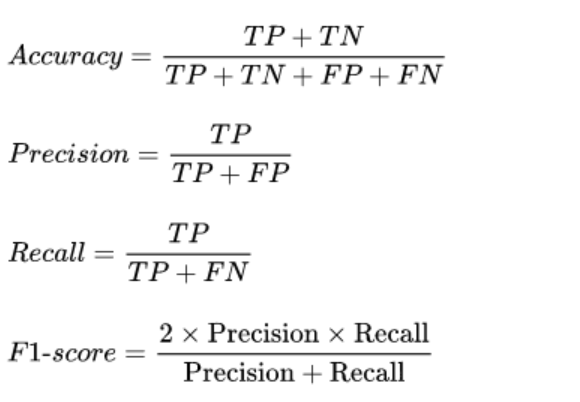
Precision measures the accuracy of the positive predictions made by the model. It is defined as the ratio of true positive (TP) instances to the total number of instances classified as positive (both true positives and false positives).
- Equation:
- Interpretation: High precision indicates a low number of false positives, meaning the model is good at predicting positive instances accurately.
Recall
Recall, also known as sensitivity or true positive rate, measures the model's ability to identify all relevant instances (true positives) from the dataset. It is defined as the ratio of true positive instances to the total number of actual positive instances (both true positives and false negatives).
- Equation:
- Interpretation: High recall indicates that the model successfully captures most of the positive instances, minimizing the number of false negatives.
F1 Score
The F1 score is the harmonic mean of precision and recall, providing a single metric that balances both. It is particularly useful when the class distribution is imbalanced and one metric alone does not provide a complete picture of the model's performance.
- Equation:
- Interpretation: The F1 score ranges from 0 to 1, with 1 being the best possible score, indicating perfect precision and recall. It is useful when you need a balance between precision and recall.
Examples and Use Cases
Consider a binary classification problem where:
- TP (True Positive): The model correctly predicts a positive instance.
- FP (False Positive): The model incorrectly predicts a positive instance.
- FN (False Negative): The model incorrectly predicts a negative instance.
Example:
Imagine a model designed to detect fraudulent transactions.
Here’s a possible confusion matrix:
| Predicted Positive | Predicted Negative | |
| Actual Positive | 70 | 30 |
| Actual Negative | 10 | 90 |
From this confusion matrix:
Choosing Between Precision, Recall, and F1 Score
- Precision: Prioritize precision when false positives are more costly than false negatives. For example, in email spam detection, marking a legitimate email as spam (false positive) is undesirable.
- Recall: Prioritize recall when false negatives are more costly than false positives. For example, in medical diagnoses, missing a positive case (false negative) can be life-threatening.
- F1 Score: Use the F1 score when you need to balance precision and recall, especially in scenarios with class imbalance.
Other Related Metrics
- Accuracy: Measures the proportion of correct predictions out of all predictions made. However, it can be misleading in imbalanced datasets.
- Specificity: Measures the proportion of actual negatives correctly identified.
- ROC-AUC: Receiver Operating Characteristic - Area Under Curve, evaluates the trade-off between true positive rate (recall) and false positive rate (1-specificity).
Conclusion
Precision, recall, and the F1 score are essential metrics for evaluating classification models in deep learning, providing insights into the model’s performance, especially in imbalanced datasets. By understanding and applying these metrics, you can better assess and improve your model’s effectiveness in real-world applications.
Enroll Now
- Python Programming
- Machine Learning