K-Fold Cross Validation
K-fold cross-validation is a technique commonly used in machine learning for assessing the performance and generalization ability of a model. It helps in estimating how well the model will perform on unseen data.
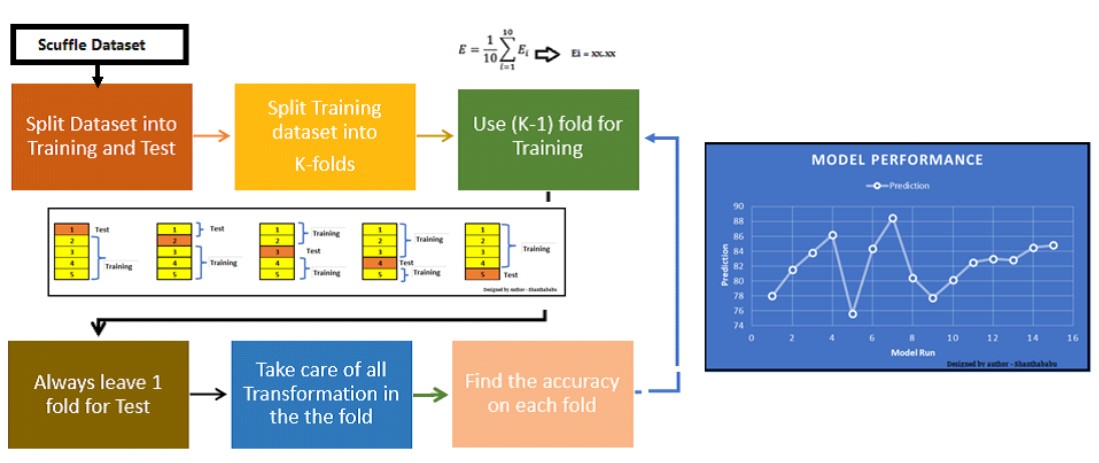
The basic idea behind K-fold cross-validation is to split the available dataset into K subsets or folds of approximately equal size. The value of K is typically chosen based on the size of the dataset and computational constraints.
The most common choice is K=10, but other values like 5 or 20 can also be used.
The K-fold cross-validation process involves the following steps: Splitting the data: The dataset is divided into K equal-sized subsets or folds. Each fold contains a similar distribution of samples from the dataset.
The splitting can be done randomly or using other strategies like stratified sampling to preserve the class distribution, depending on the nature of the data. Training and evaluation:
For each iteration, one of the K folds is selected as the validation set, and the remaining K-1 folds are used as the training set. The model is trained on the training set and evaluated on the validation set.
This process is repeated K times, with each fold serving as the validation set once.
Performance measurement: The performance metric of interest, such as accuracy, precision, recall, or F1-score, is computed for each iteration using the predictions made on the validation set. The average performance across all K iterations is then calculated to get an estimate of the model's performance.
Model selection and tuning: K-fold cross-validation can be used for model selection and hyperparameter tuning. Different models or different sets of hyperparameters can be evaluated using the cross-validation process, and the best-performing model or parameter configuration can be selected based on the average performance across the K iterations.
Final model training: Once the model and hyperparameters are selected, the final model can be trained on the entire dataset using the chosen configuration. This model is then ready to be deployed and used for making predictions on new, unseen data. K-fold cross-validation provides a more robust estimate of a model's performance compared to a single train-test split, as it uses multiple train-test splits and averages the results.
It helps in assessing how well the model generalizes to unseen data and reduces the risk of overfitting or underfitting. Note that there are variations of cross-validation techniques, such as stratified K-fold cross-validation and leave-one-out cross-validation, which have specific use cases and advantages.
The choice of the appropriate cross-validation technique depends on the dataset and the specific problem at hand.
Enroll Now
- Python Programming
- Machine Learning