Logistic Regression

Logistic regression is a widely used supervised machine learning algorithm used for binary and multiclass classification tasks. Despite its name, it is a classification algorithm rather than a regression one.

Logistic regression models the probability that a given input belongs to a particular class. It's especially useful when you want to predict the probability of an event happening, given a set of independent variables.

Overview of logistic regression:

1. Binary Classification:

   • In binary logistic regression, the target variable (dependent variable) is binary, meaning it has only two possible classes, often labeled as 0 and 1, or "negative" and "positive."
   • The logistic regression model estimates the probability that an input sample belongs to the positive class.

2. Multiclass Classification:

   • Logistic regression can also be extended to multiclass classification problems, where the target variable can have more than two classes. In this case, it's called "multinomial logistic regression" or "softmax regression."
   • The model calculates the probability distribution across all classes and assigns an input sample to the class with the highest estimated probability.

3. Logistic Function (Sigmoid Function):

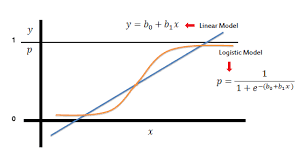
   • Logistic regression uses the logistic function (also known as the sigmoid function) to transform a linear combination of input features into a value between 0 and 1. The formula for the logistic function is:

     P(Y=1|X) = 1 / (1 + e^(-z))

     • P(Y=1|X) is the probability that the target variable equals 1 (positive class) given the input features X.
     • z is the linear combination of input features and model coefficients.

4. Model Parameters:

   • Logistic regression has parameters (coefficients) associated with each independent variable, and it learns these parameters from the training data through methods like maximum likelihood estimation.
   • The model also includes an intercept term, similar to linear regression.

5. Training and Optimization:

   • Logistic regression aims to find the best-fitting model parameters that maximize the likelihood of the observed data given the model. This is typically done through optimization techniques like gradient descent.

6. Decision Boundary:

   • The decision boundary in logistic regression is the line (for binary classification) or hyperplane (for multiclass classification) that separates the classes. It is determined by the model parameters and is typically set at a probability threshold (e.g., 0.5 for binary classification).

7. Model Evaluation:

   • Logistic regression models are evaluated using metrics such as accuracy, precision, recall, F1-score, and area under the receiver operating characteristic curve (AUC-ROC) to assess their classification performance.

8. Regularization:

   • To prevent overfitting, logistic regression models can incorporate regularization techniques such as L1 (Lasso) and L2 (Ridge) regularization, which add penalty terms to the loss function.

Logistic regression is a fundamental algorithm in machine learning, particularly in classification tasks. It is interpretable and relatively simple to implement, making it a good choice for many real-world problems.

However, it assumes a linear relationship between input features and the log-odds of the class probabilities, which may not always hold true for complex data.

In such cases, more advanced models like decision trees, random forests, or deep neural networks may be considered.

Logistic Regression

• Python Programming
• Machine Learning