Machine Learning Training and Testing Data Linear Regression Logistic Regression Decision Tree Support Vector Machine Random Forest Algorithm K-Fold Cross Validation K-Mean Clustering K-Nearest Neighbors Algorithm Hyperparameter Tuning Navie Bayes Classifier Time Series Analysis Ensemble Learning Genetic Algorithm Reinforcement Learning Machine Learning Quiz

Linear Regression

Linear regression is a fundamental supervised machine learning algorithm used for modeling the relationship between a dependent variable (target) and one or more independent variables (features or predictors).

Its primary objective is to establish a linear relationship between the input variables and the output variable. Linear regression is widely employed for tasks like predicting numerical values, such as stock prices, temperature, or sales figures.

Key components and concepts associated with linear regression:

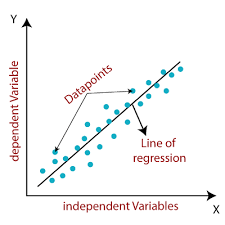
  1. Linear Relationship:

    • Linear regression assumes that the relationship between the independent variables (features) and the dependent variable (target) is approximately linear. It models this relationship as a straight line equation.

  2. Simple Linear Regression:

    • In simple linear regression, there is only one independent variable, denoted as "x." The linear relationship is expressed as:

      y = mx + b

      • y is the dependent variable (target).
      • x is the independent variable (feature).
      • m is the slope of the line (the coefficient representing the relationship between x and y).
      • b is the y-intercept (the point where the line intersects the y-axis).

  3. Multiple Linear Regression:

    • In multiple linear regression, there are multiple independent variables (features). The linear relationship is extended to accommodate multiple predictors:

      y = b0 + b1*x1 + b2*x2 + ... + bn*xn

      • y is the dependent variable (target).
      • x1, x2, ..., xn are the independent variables (features).
      • b0 is the intercept.
      • b1, b2, ..., bn are the coefficients associated with each feature.

  4. Fitting the Model:

    • The goal of linear regression is to find the best-fitting line (or hyperplane in the case of multiple linear regression) that minimizes the sum of squared errors between the predicted values and the actual target values in the training data.

  5. Parameters Estimation:

    • To estimate the model parameters (coefficients), various methods can be used, with the most common being the method of least squares. This method aims to minimize the sum of the squared differences between the predicted values and the actual target values.

  6. Model Evaluation:

    • Linear regression models are evaluated using metrics like mean squared error (MSE), mean absolute error (MAE), and R-squared (coefficient of determination) to assess how well the model fits the data and makes predictions.

  7. Assumptions:

    • Linear regression assumes that the data satisfies certain assumptions, including linearity, independence of errors, homoscedasticity (constant variance of errors), and normally distributed errors. Violations of these assumptions can affect the model's performance.

  8. Regularization:

    • To handle multicollinearity (high correlation between predictors) and prevent overfitting, variants of linear regression, such as Ridge and Lasso regression, introduce regularization terms into the model.

Linear regression is a simple yet powerful tool for understanding and modeling relationships in data.

While it may not capture complex nonlinear relationships, it serves as a foundation for more advanced regression techniques and is widely used in various fields, including economics, finance, and the natural and social sciences.

Linear Regression


Enroll Now

  • Python Programming
  • Machine Learning